Geotechnical Engineering-I [Lec #27A: Flow Calculation From Flow Nets]
•
2 likes•1,521 views
Class notes of Geotechnical Engineering course I used to teach at UET Lahore. Feel free to download the slide show. Anyone looking to modify these files and use them for their own teaching purposes can contact me directly to get hold of editable version.
Report
Share
Report
Share
Download to read offline
Recommended
Recommended
More Related Content
What's hot
What's hot (20)
Bearing capacity of shallow foundations by abhishek sharma 

Bearing capacity of shallow foundations by abhishek sharma
Numerical problem on bearing capacity is code terzaghi water table (usefulsea...

Numerical problem on bearing capacity is code terzaghi water table (usefulsea...
Geotechnical Engineering-I [Lec #24: Soil Permeability - II]![Geotechnical Engineering-I [Lec #24: Soil Permeability - II]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-I [Lec #24: Soil Permeability - II]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-I [Lec #24: Soil Permeability - II]
Geotechnical Engineering-I [Lec #21: Consolidation Problems]![Geotechnical Engineering-I [Lec #21: Consolidation Problems]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-I [Lec #21: Consolidation Problems]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-I [Lec #21: Consolidation Problems]
Numerical Question on Terzaghi Bearing Capacity Theory, Meyerhof Bearing Capa...

Numerical Question on Terzaghi Bearing Capacity Theory, Meyerhof Bearing Capa...
Question and Answers on Terzaghi’s Bearing Capacity Theory (usefulsearch.org)...

Question and Answers on Terzaghi’s Bearing Capacity Theory (usefulsearch.org)...
Similar to Geotechnical Engineering-I [Lec #27A: Flow Calculation From Flow Nets]
Similar to Geotechnical Engineering-I [Lec #27A: Flow Calculation From Flow Nets] (20)
Calculation of Fluid Dynamic for Wind Flow around Reinforced Concrete Walls

Calculation of Fluid Dynamic for Wind Flow around Reinforced Concrete Walls
23Network FlowsAuthor Arthur M. Hobbs, Department of .docx

23Network FlowsAuthor Arthur M. Hobbs, Department of .docx
soil mechanics and its behaviour andPermeability in Stratified Soil Layers

soil mechanics and its behaviour andPermeability in Stratified Soil Layers
More from Muhammad Irfan
More from Muhammad Irfan (20)
Geotechnical Engineering-II [Lec #28: Finite Slope Stability Analysis]![Geotechnical Engineering-II [Lec #28: Finite Slope Stability Analysis]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #28: Finite Slope Stability Analysis]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #28: Finite Slope Stability Analysis]
Geotechnical Engineering-II [Lec #26: Slope Stability]![Geotechnical Engineering-II [Lec #26: Slope Stability]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #26: Slope Stability]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #26: Slope Stability]
Geotechnical Engineering-II [Lec #27: Infinite Slope Stability Analysis]![Geotechnical Engineering-II [Lec #27: Infinite Slope Stability Analysis]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #27: Infinite Slope Stability Analysis]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #27: Infinite Slope Stability Analysis]
Geotechnical Engineering-II [Lec #25: Coulomb EP Theory - Numericals]![Geotechnical Engineering-II [Lec #25: Coulomb EP Theory - Numericals]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #25: Coulomb EP Theory - Numericals]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #25: Coulomb EP Theory - Numericals]
Geotechnical Engineering-II [Lec #24: Coulomb EP Theory]![Geotechnical Engineering-II [Lec #24: Coulomb EP Theory]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #24: Coulomb EP Theory]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #24: Coulomb EP Theory]
Geotechnical Engineering-II [Lec #23: Rankine Earth Pressure Theory]![Geotechnical Engineering-II [Lec #23: Rankine Earth Pressure Theory]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #23: Rankine Earth Pressure Theory]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #23: Rankine Earth Pressure Theory]
Geotechnical Engineering-II [Lec #22: Earth Pressure at Rest]![Geotechnical Engineering-II [Lec #22: Earth Pressure at Rest]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #22: Earth Pressure at Rest]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #22: Earth Pressure at Rest]
Geotechnical Engineering-II [Lec #21: Lateral Earth Pressure)

Geotechnical Engineering-II [Lec #21: Lateral Earth Pressure)
Geotechnical Engineering-II [Lec #20: WT effect on Bearing Capcity)

Geotechnical Engineering-II [Lec #20: WT effect on Bearing Capcity)
Geotechnical Engineering-II [Lec #19: General Bearing Capacity Equation]![Geotechnical Engineering-II [Lec #19: General Bearing Capacity Equation]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #19: General Bearing Capacity Equation]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #19: General Bearing Capacity Equation]
Geotechnical Engineering-II [Lec #18: Terzaghi Bearing Capacity Equation]![Geotechnical Engineering-II [Lec #18: Terzaghi Bearing Capacity Equation]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #18: Terzaghi Bearing Capacity Equation]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #18: Terzaghi Bearing Capacity Equation]
Geotechnical Engineering-II [Lec #17: Bearing Capacity of Soil]![Geotechnical Engineering-II [Lec #17: Bearing Capacity of Soil]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #17: Bearing Capacity of Soil]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #17: Bearing Capacity of Soil]
Geotechnical Engineering-II [Lec #15 & 16: Schmertmann Method]![Geotechnical Engineering-II [Lec #15 & 16: Schmertmann Method]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #15 & 16: Schmertmann Method]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #15 & 16: Schmertmann Method]
Geotechnical Engineering-II [Lec #14: Timoshenko & Goodier Method]![Geotechnical Engineering-II [Lec #14: Timoshenko & Goodier Method]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #14: Timoshenko & Goodier Method]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #14: Timoshenko & Goodier Method]
Geotechnical Engineering-II [Lec #13: Elastic Settlements]![Geotechnical Engineering-II [Lec #13: Elastic Settlements]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #13: Elastic Settlements]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #13: Elastic Settlements]
Geotechnical Engineering-II [Lec #12: Consolidation Settlement Computation]![Geotechnical Engineering-II [Lec #12: Consolidation Settlement Computation]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #12: Consolidation Settlement Computation]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #12: Consolidation Settlement Computation]
Geotechnical Engineering-II [Lec #11: Settlement Computation]![Geotechnical Engineering-II [Lec #11: Settlement Computation]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #11: Settlement Computation]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #11: Settlement Computation]
Geotechnical Engineering-II [Lec #9+10: Westergaard Theory]![Geotechnical Engineering-II [Lec #9+10: Westergaard Theory]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #9+10: Westergaard Theory]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #9+10: Westergaard Theory]
Geotechnical Engineering-II [Lec #8: Boussinesq Method - Rectangular Areas]![Geotechnical Engineering-II [Lec #8: Boussinesq Method - Rectangular Areas]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #8: Boussinesq Method - Rectangular Areas]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #8: Boussinesq Method - Rectangular Areas]
Geotechnical Engineering-II [Lec #7: Soil Stresses due to External Load]![Geotechnical Engineering-II [Lec #7: Soil Stresses due to External Load]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Geotechnical Engineering-II [Lec #7: Soil Stresses due to External Load]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Geotechnical Engineering-II [Lec #7: Soil Stresses due to External Load]
Recently uploaded
Call Girl Meerut Indira Call Now: 8617697112 Meerut Escorts Booking Contact Details WhatsApp Chat: +91-8617697112 Meerut Escort Service includes providing maximum physical satisfaction to their clients as well as engaging conversation that keeps your time enjoyable and entertaining. Plus they look fabulously elegant; making an impressionable. Independent Escorts Meerut understands the value of confidentiality and discretion - they will go the extra mile to meet your needs. Simply contact them via text messaging or through their online profiles; they'd be more than delighted to accommodate any request or arrange a romantic date or fun-filled night together. We provide –(INDIRA) Call Girl Meerut Call Now 8617697112 Meerut Escorts 24x7

(INDIRA) Call Girl Meerut Call Now 8617697112 Meerut Escorts 24x7Call Girls in Nagpur High Profile Call Girls
From customer value engagements to hands-on production support, our Services span across every stage of our customers digital transformation journey, to help ensure that every customer is successful in their adoption of our solutions.
• Implementation, Upgrade, Migration, and Maintenance Services
• On-Premises and On-Cloud
• COTS Training Services; On-Site and Virtual
• Software Support Services; Legacy and 3DEXPERIENCE
• Value Engagement & Blueprinting
• Specialized Consulting and Support Services
• Customized Training Services
• Automation and Configuration Services
• Technical Resource Augmentation Services
• Project Management
• Know-how Training (mentoring) and Resource AugmentationNavigating Complexity: The Role of Trusted Partners and VIAS3D in Dassault Sy...

Navigating Complexity: The Role of Trusted Partners and VIAS3D in Dassault Sy...Arindam Chakraborty, Ph.D., P.E. (CA, TX)
Call girls in delhi ✔️✔️🔝 9953056974 🔝✔️✔️Welcome To Vip Escort Services In Delhi [ ]Noida Gurgaon 24/7 Open Sex Escort Services With Happy Ending ServiCe Done By Most Attractive Charming Soft Spoken Bold Beautiful Full Cooperative Independent Escort Girls ServiCe In All-Star Hotel And Home Service In All Over Delhi, Noida, Gurgaon, Faridabad, Ghaziabad, Greater Noida,
• IN CALL AND OUT CALL SERVICE IN DELHI NCR
• 3* 5* 7* HOTELS SERVICE IN DELHI NCR
• 24 HOURS AVAILABLE IN DELHI NCR
• INDIAN, RUSSIAN, PUNJABI, KASHMIRI ESCORTS
• REAL MODELS, COLLEGE GIRLS, HOUSE WIFE, ALSO AVAILABLE
• SHORT TIME AND FULL TIME SERVICE AVAILABLE
• HYGIENIC FULL AC NEAT AND CLEAN ROOMS AVAIL. IN HOTEL 24 HOURS
• DAILY NEW ESCORTS STAFF AVAILABLE
• MINIMUM TO MAXIMUM RANGE AVAILABLE.
Call Girls in Delhi & Independent Escort Service –
CALL GIRLS SERVICE DELHI NCR
Vip call girls in Delhi
Call Girls in Delhi, Call Girl Service 24×7 open
Call Girls in Delhi Best Delhi Escorts in Delhi
Low Rate Call Girls In Saket Delhi
X~CALL GIRLS IN Ramesh Nagar Metro
best Delhi call girls and Delhi escort service.
CALL GIRLS SERVICE IN ALL DELHI …
(Delhi) Call Girls in (Chanakyapuri)
Hot And Sexy Independent Model Escort Service In Delhi Unlimited Enjoy Genuine 100% Profiles And Trusted Door Step Call Girls Feel Free To Call Us Female Service Hot Busty & Sexy Party Girls Available For Complete Enjoyment. We Guarantee Full Satisfaction & In Case Of Any Unhappy Experience, We Would Refund Your Fees, Without Any Questions Asked. Feel Free To Call Us Female Service Provider Hours Opens Thanks.
Delhi Escorts Services 100% secure Services.Incall_OutCall Available and outcall Services provide.
We are available 24*7 for Full Night and short Time Escort Services all over Delhi NCR.
Delhi All Hotel Services available 3* 4* 5* Call Call
Delhi Escorts Services And Delhi Call Girl Agency 100% secure Services in my agency. Incall and outcall Services provide.
We are available 24*7 for Full Night and short Time Escort Services my agency in all over New Delhi
Delhi All Hotel Services available my agency
SERVICES [✓✓✓]
Housewife
College Girl
VIP Escort
Independent Girl
Aunty
Without a Condom sucking )?
Sexy Aunty.DSL (Dick Sucking Lips)?
DT (Dining at the Toes English Spanking)
Doggie (Sex style from no behind)??
OutCall- All Over Delhi Noida Gurgaon 24/7
FOR APPOINTMENT Call/Whatsop / 9953056974Call Girls in Ramesh Nagar Delhi 💯 Call Us 🔝9953056974 🔝 Escort Service

Call Girls in Ramesh Nagar Delhi 💯 Call Us 🔝9953056974 🔝 Escort Service9953056974 Low Rate Call Girls In Saket, Delhi NCR
Welcome to the April edition of WIPAC Monthly, the magazine brought to you by Water Industry Process Automation & Control.
In this month's edition, along with the latest news from the industry we have articles on:
The use of artificial intelligence and self-service platforms to improve water sustainability
A feature article on measuring wastewater spills
An article on the National Underground Asset Register
Have a good month,
OliverWater Industry Process Automation & Control Monthly - April 2024

Water Industry Process Automation & Control Monthly - April 2024Water Industry Process Automation & Control
Recently uploaded (20)
(INDIRA) Call Girl Meerut Call Now 8617697112 Meerut Escorts 24x7

(INDIRA) Call Girl Meerut Call Now 8617697112 Meerut Escorts 24x7
Design For Accessibility: Getting it right from the start

Design For Accessibility: Getting it right from the start
Bhosari ( Call Girls ) Pune 6297143586 Hot Model With Sexy Bhabi Ready For ...

Bhosari ( Call Girls ) Pune 6297143586 Hot Model With Sexy Bhabi Ready For ...
Call Girls Walvekar Nagar Call Me 7737669865 Budget Friendly No Advance Booking

Call Girls Walvekar Nagar Call Me 7737669865 Budget Friendly No Advance Booking
Intze Overhead Water Tank Design by Working Stress - IS Method.pdf

Intze Overhead Water Tank Design by Working Stress - IS Method.pdf
Call Girls Pimpri Chinchwad Call Me 7737669865 Budget Friendly No Advance Boo...

Call Girls Pimpri Chinchwad Call Me 7737669865 Budget Friendly No Advance Boo...
VIP Call Girls Ankleshwar 7001035870 Whatsapp Number, 24/07 Booking

VIP Call Girls Ankleshwar 7001035870 Whatsapp Number, 24/07 Booking
Navigating Complexity: The Role of Trusted Partners and VIAS3D in Dassault Sy...

Navigating Complexity: The Role of Trusted Partners and VIAS3D in Dassault Sy...
Call Girls in Ramesh Nagar Delhi 💯 Call Us 🔝9953056974 🔝 Escort Service

Call Girls in Ramesh Nagar Delhi 💯 Call Us 🔝9953056974 🔝 Escort Service
chapter 5.pptx: drainage and irrigation engineering

chapter 5.pptx: drainage and irrigation engineering
Double Revolving field theory-how the rotor develops torque

Double Revolving field theory-how the rotor develops torque
Top Rated Call Girls In chittoor 📱 {7001035870} VIP Escorts chittoor

Top Rated Call Girls In chittoor 📱 {7001035870} VIP Escorts chittoor
Water Industry Process Automation & Control Monthly - April 2024

Water Industry Process Automation & Control Monthly - April 2024
FULL ENJOY Call Girls In Mahipalpur Delhi Contact Us 8377877756

FULL ENJOY Call Girls In Mahipalpur Delhi Contact Us 8377877756
Call Girls Wakad Call Me 7737669865 Budget Friendly No Advance Booking

Call Girls Wakad Call Me 7737669865 Budget Friendly No Advance Booking
Geotechnical Engineering-I [Lec #27A: Flow Calculation From Flow Nets]
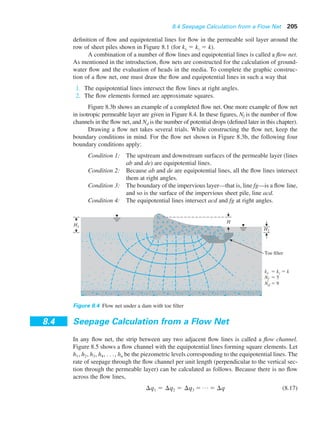
- 1. 8.4 Seepage Calculation from a Flow Net 205 definition of flow and equipotential lines for flow in the permeable soil layer around the row of sheet piles shown in Figure 8.1 (for kx ϭ kz ϭ k). A combination of a number of flow lines and equipotential lines is called a flow net. As mentioned in the introduction, flow nets are constructed for the calculation of ground- water flow and the evaluation of heads in the media. To complete the graphic construc- tion of a flow net, one must draw the flow and equipotential lines in such a way that 1. The equipotential lines intersect the flow lines at right angles. 2. The flow elements formed are approximate squares. Figure 8.3b shows an example of a completed flow net. One more example of flow net in isotropic permeable layer are given in Figure 8.4. In these figures, Nf is the number of flow channels in the flow net, and Nd is the number of potential drops (defined later in this chapter). Drawing a flow net takes several trials. While constructing the flow net, keep the boundary conditions in mind. For the flow net shown in Figure 8.3b, the following four boundary conditions apply: Condition 1: The upstream and downstream surfaces of the permeable layer (lines ab and de) are equipotential lines. Condition 2: Because ab and de are equipotential lines, all the flow lines intersect them at right angles. Condition 3: The boundary of the impervious layer—that is, line fg—is a flow line, and so is the surface of the impervious sheet pile, line acd. Condition 4: The equipotential lines intersect acd and fg at right angles. Toe filter kx ϭ kz ϭ k Nf ϭ 5 Nd ϭ 9 H1 H2 H Figure 8.4 Flow net under a dam with toe filter 8.4 Seepage Calculation from a Flow Net In any flow net, the strip between any two adjacent flow lines is called a flow channel. Figure 8.5 shows a flow channel with the equipotential lines forming square elements. Let h1, h2, h3, h4, . . ., hn be the piezometric levels corresponding to the equipotential lines. The rate of seepage through the flow channel per unit length (perpendicular to the vertical sec- tion through the permeable layer) can be calculated as follows. Because there is no flow across the flow lines, (8.17)¢q1 ϭ ¢q2 ϭ ¢q3 ϭ p ϭ ¢q
- 2. 206 Chapter 8: Seepage From Darcy’s law, the flow rate is equal to kiA. Thus, Eq. (8.17) can be written as (8.18) Eq. (8.18) shows that if the flow elements are drawn as approximate squares, the drop in the piezometric level between any two adjacent equipotential lines is the same. This is called the potential drop. Thus, (8.19) and (8.20) In Figure 8.3b, for any flow channel, H ϭ H1 Ϫ H2 and Nd ϭ 6. If the number of flow channels in a flow net is equal to Nf , the total rate of flow through all the channels per unit length can be given by (8.21) Although drawing square elements for a flow net is convenient, it is not always nec- essary. Alternatively, one can draw a rectangular mesh for a flow channel, as shown in Figure 8.6, provided that the width-to-length ratios for all the rectangular elements in the flow net are the same. In this case, Eq. (8.18) for rate of flow through the channel can be modified to (8.22) If b1/l1 ϭ b2/l2 ϭ b3/l3 n (i.e., the elements are not square), Eqs. (8.20) and (8.21) can be modified to (8.23)¢q ϭ kHa n Nd b ϭ p ϭ ¢q ϭ ka h1 Ϫ h2 l1 bb1 ϭ ka h2 Ϫ h3 l2 bb2 ϭ ka h3 Ϫ h4 l3 bb3 ϭ p q ϭ k HNf Nd Nd ϭ number of potential drops where H ϭ head difference between the upstream and downstream sides ¢q ϭ k H Nd h1 Ϫ h2 ϭ h2 Ϫ h3 ϭ h3 Ϫ h4 ϭ p ϭ H Nd ¢q ϭ ka h1 Ϫ h2 l1 bl1 ϭ ka h2 Ϫ h3 l2 bl2 ϭ ka h3 Ϫ h4 l3 bl3 ϭ p h1 h2 h3 h4 ⌬q l3 l2 l1 ⌬q ⌬q2 ⌬q3 ⌬q1 l3 l2 l1 Figure 8.5 Seepage through a flow channel with square elements
- 3. 8.4 Seepage Calculation from a Flow Net 207 h1 h2 h3 h4 ⌬q l3 l2 l1 ⌬q ⌬q2 ⌬q3 ⌬q1 b3 b2 b1 Figure 8.6 Seepage through a flow channel with rectangular elements and (8.24) Figure 8.7 shows a flow net for seepage around a single row of sheet piles. Note that flow channels 1 and 2 have square elements. Hence, the rate of flow through these two channels can be obtained from Eq. (8.20): However, flow channel 3 has rectangular elements. These elements have a width-to-length ratio of about 0.38; hence, from Eq. (8.23) ¢q3 ϭ k Nd H10.382 ¢q1 ϩ ¢q2 ϭ k Nd H ϩ k Nd H ϭ 2kH Nd q ϭ kHa Nf Nd bn Impervious layer Water level Water table 5 m Flow channel 1 ϭ 1 l b Flow channel 2 ϭ 1 l b Ground surface Scale Flow channel 3 l b 1 0.38 Ϸ 5.6 m 2.2 m a 4.1 m d c H e b Figure 8.7 Flow net for seepage around a single row of sheet piles
- 4. So, the total rate of seepage can be given as (8.25)q ϭ ¢q1 ϩ ¢q2 ϩ ¢q3 ϭ 2.38 kH Nd Example 8.2 A flow net for flow around a single row of sheet piles in a permeable soil layer is shown in Figure 8.7. Given that kx ϭ kz ϭ k ϭ 5 ϫ 10Ϫ3 cm/sec, determine a. How high (above the ground surface) the water will rise if piezometers are placed at points a and b. b. The total rate of seepage through the permeable layer per unit length c. The approximate average hydraulic gradient at c. Solution Part a From Figure 8.7, we have Nd ϭ 6, H1 ϭ 5.6 m, and H2 ϭ 2.2 m. So the head loss of each potential drop is At point a, we have gone through one potential drop. So the water in the piezome- ter will rise to an elevation of (5.6 Ϫ 0.567) ϭ 5.033 m above the ground surface At point b, we have five potential drops. So the water in the piezometer will rise to an elevation of [5.6 Ϫ (5)(0.567)] ϭ 2.765 m above the ground surface Part b From Eq. (8.25), Part c The average hydraulic gradient at c can be given as (Note: The average length of flow has been scaled.) ■ i ϭ head loss average length of flow between d and e ϭ ¢H ¢L ϭ 0.567m 4.1m ϭ 0.138 ϭ 6.74 ϫ 10Ϫ5 m3 /sec/m q ϭ 2.38 k1H1 Ϫ H2 2 Nd ϭ 12.38215 ϫ 10Ϫ5 m/sec215.6 Ϫ 2.22 6 ¢H ϭ H1 Ϫ H2 Nd ϭ 5.6 Ϫ 2.2 6 ϭ 0.567m 208 Chapter 8: Seepage