VECTORES: Bachillerato y Nivel Cero B (ESPOL)

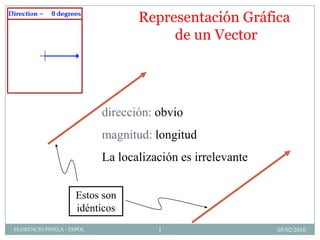
Representación Gráfica
de un Vector

dirección: obvio
magnitud: longitud
La localización es irrelevante

Estos son
idénticos
FLORENCIO PINELA - ESPOL 1 05/02/2010

¿Por qué es importante la dirección de
una cantidad vectorial?
La misma rapidez (escalar)
del viento, pero distinta
velocidad (vector)

¿Qué preguntaría el piloto a la torre de control, si de ésta le indican
que el viento sopla en el aeropuerto a 40 km/h?

Representación de un vector en
Coordenadas Rectangulares
Cualquier vector A que se encuentre en el plano
x-y es posible representarlo por medio de sus
componentes rectangulares Ax y Ay
   !Cuidado! A2 2
Ax 2
Ay
A Ax Ay Ax 4 
A A Ax2 Ay
2
Ay 3
  
A Ax Ay 7 Ax = A cos
A
Ay Ay = A sen
Ay 1
Ay
tan tan
Ax Ax Ax

Representación de un vector en
Coordenadas Polares
Algunas veces es más conveniente representar un punto en el plano
por sus coordenadas polares, (r, ) donde r es la distancia desde el
origen hasta el punto de coordenadas (x,y) y es el ángulo entre r y
un eje fijo, medido contrario a las manecillas del reloj.
y y
(x,y) tan
x
r 1 y
tan
x

x 2 2
o r x y
05/02/2010 FLORENCIO PINELA - ESPOL 4

La dirección de un vector en 2-D
y
Sea = 130
Sen 130 = 0,766
Cos 130 = -0,643

x
-α
α = - 230
Sen(-230 )= 0,766
Cos(-230 )=-0,643
• Positivo en “sentido” antihorario
• Negativo en “sentido” horario

Ejemplo: Encuentre el vector en coordenadas polares
si sus coordenadas en el plano x-y son (-2, -5)

¡Cuidado cuando use
tan = y/x !

' 1 5
tan 68, 2o
2
-2
¡Línea de acción del
vector!
r o o
180 68, 2
-5
 r ( 2)2 ( 5)2 29
r : 29; 248, 2o

El Método Gráfico para la Suma de Vectores

C Los vectores se unen
B
extremo con origen,
A+B conservando su
A+B+C magnitud y dirección.
El vector resultante
A parte del origen del
primero al extremo
del último
D
R
R = A + B +C + D
    
R A B C D
Florencio Pinela

EL VECTOR NEGATIVO
LA MAGNITUD O MODULO DE UN VECTOR ES
SIEMPRE UNA CANTIDAD POSITIVA.

Un vector es negativo cuando
apunta en dirección contraria a uno
definido como positivo.
Cuando un vector NO está referido a un
sistema de coordenadas.

B C
A -A -B

-C


RESTA DE VECTORES
RESTARLE UN VECTOR A OTRO VECTOR ES
EQUIVALENTE A SUMARLE SU VECTOR NEGATIVO

A – B = A + (- B)

A B

Del extremo de B al
extremo de A
A-B
A-B

Polígono Unamos los vectores por su origen


Pregunta de concepto

Para los vectores a, b y c, indicados en la
figura. ¿Cuál de las siguientes alternativas es
correcta?
  
1) a c b
   a
2) a b c
   c
3) c b a
4) Todas son correctas b


LA LEY DEL COSENO
• Sean los vectores a y b

Sea el menor ángulo formado entre los vectores
unidos por su origen
Sea el ángulo formado entre los vectores unidos
extremo con origen

b
b

a a

Sea R el vector resultante de sumar el vector a con el vector
b, esto es R = a + b, y el angulo formado entre a y b
unidos por su origen.

R b sen
b

a
b cos

R2 = (a + b cos )2 + (b sen )2
R2 = a2+ b2cos2 + 2abcos + b2 sen2

R2 = a2 + b2 + 2ab cos

La ley del coseno en función del ángulo α

R
b

a
R2 = a2 + b2 + 2ab Cos
= 180 -
cos = cos (180 - ) = - cos

R2 = a2 + b2 - 2ab Cos

Sea P el vector resultante de la diferencia
entre los vector a y b, y sea R la resultante
de la suma entre a y b.
R
b
P
P=a-b
a R=a+b

R2 = a2 + b2 + 2ab Cos
P2 = a2 + b2 - 2ab Cos
Recuerde que la magnitud del vector a –b es igual
a la magnitud del vector b – a

Vectores Unitarios:
 Un Vector Unitario es un vector
que tiene magnitud 1 y no tiene
unidades U
 Es usado para especificar una
dirección û

 Un vector unitario u apunta en la
y
dirección de U
A menudo denotado con un j
“sombrero”: u = û
x
 Ejemplos útiles son los vectores k i
z
unitarios cartesianos [ i, j, k ]
 apuntando en las direcciones
de los ejes x, y y z

LOS VECTORES UNITARIOS i, j y k
Un vector unitario es la relación entre el vector
y su magnitud 
U
ˆ
u
U
   
y
A Ax Ay Az

j A ˆ
Ax i Ay ˆ
j ˆ
Az k
k i x

z

Suma de Vectores usando
componentes:
 Considere C = A + B.

(a) C = (Ax i + Ay j) + (Bx i + By j) = (Ax + Bx)i + (Ay + By)j
(b) C = (Cx i + Cy j)

 Comparando las componentes de (a) y (b):

 Cx = Ax + Bx C By
B
 Cy = Ay + By
A Ay Bx
Ax

Cualquier vector puede ser expresado en
término de vectores unitarios.

A = Ax i + Ay j + Az k
Se pueden sumar, restar y multiplicar

Sean los vectores A= 2i – 4j + 6k y B= 4i + 2j – 3k
 
A B = 6i – 2j + 3k
 
A B = - 2i – 6j + 9k
 
A 2B = 10i

B
A

C

Exprese los vectores de la figura en función de vectores unitarios
05/02/2010 FLORENCIO PINELA - ESPOL
19

B
A

C

Para los vectores de la figura realice la siguiente operación:
A + B – 2C
20 05/02/2010
FLORENCIO PINELA - ESPOL

Proyeción de un Vector en Tres
Dimensiones
 Cualquier vector en tres
dimensiones puede ser
proyectado sobre el plano x-y.
z
 La proyección del vector forma
 
un ángulo con el eje de las x. a a
 Ahora proyecte el vector sobre
el eje de las z.
 El vector original forma un
ángulo con el eje z. y

x

Una Nota sobre la regla de la mano derecha
en el sistema de coordenadas
 Un sistema de
coordenadas en tres z
dimensiones debe
obedecer la reglas de la
mano derecha.
 Doble los dedos de su
MANO DERECHA de tal y
forma que vayan desde x
hasta y. Su pulgar x
apuntará en la dirección z.

September 5, 2007

Right Handed Coordinate Systems
Which of these coordinate
systems obey the right-hand I. II.
rule?
y y
A. I and II.
B. II and III. x z
C. I, II, and III.
z x
D. I and IV.
x x
E. IV only. III. IV.
y z
z y

September 5, 2007

Las componentes ortogonales del vector A
en tres dimensiones (3D).
y

Ayj
A

Ax i
x
Az k


z A ˆ j ˆ
Axi Ay ˆ Az k A 2
A
x A 2
y A 2
z


Exprese el vector indicado en la figura en
función de sus componentes rectangulares
i, j k. A = 10 i – 8 j + 4 k
y 10 i
¿Cuál sería la magnitud
del vector A?

A 8 A A 102 82 42

-8j

4 x
10 4k
z

Determine la magnitud de los vectores A, B y C

2 2 C
A 5 8
8

2 2 A B
B 8 6
2 2 2
C 5 6 8 6
5


Para el paralelepípedo de la figura, determine el ángulo
formado entre los vectores a y b.

y
a) 45,0º
b) 48,2º 6

a
c) 50,2º x
b
4
d) 53,8º
z 5
e) 55,2º


Solución:

     y

R a b b a R
6
a
x
2 2 2 b
R a b 2ab cos 4
z 5
a 2 b2 R 2
Cos a 42 62
2ab
o b 52 6 2
50, 2
R2 52 4 2


y Otra solución
a = 6j – 4k => a2 = 62 +42 => a = = 7,21
6 b = 5i + 6j => b2 = 52 + 62 => b = = 7,81
a
b
x Llamamos c al vector (a + b) = 5i + 12j – 4k
4

z 5
c = 13,60
a) 45,0º Utilizando la ley del coseno
b) 48,2º C2 = a2 + b2 + 2ab cos
c) 50,2º Despejando el coseno de y reemplazando los
d) 53,8º módulos de los vectores a,b y c
e) 55,2º Cos = (185-52-61)/112,62
Cos = 0,64

Por tanto es igual a 50,2

LA LEY DEL SENO
PQ
Sen
c a
b PQ
Sen
a b
R RS
Sen
P c
RS
Sen
S b
Q

Sen Sen

PQ RS
Sen Sen
a aSen bSen c
cSen bSen
PQ RS
Sen Sen
b b

Sen sen Sen Sen
b a b c

Sen Sen Sen
a b c
a b c
Sen Sen Sen

LA LEY DEL SENO

c
b
a

Sen Sen Sen
a b c
a b c
Sen Sen Sen

Utilice la ley del seno para determinar los valores
de las tensiones de cada una de las cuerdas.

T1
40 T2

20

100 N T3

33

T2
70
T1 70
40
T3
T2 T1
40

20

T3 T1
100 N sen70o sen70o
T3=100 N

T3 T2 sen40o
T3 T1 100 N
T2 100 N
sen70o sen40o sen70o
34

El Método Analítico para
la Suma de Vectores
• El método geométrico de suma de vectores NO es el
procedimiento recomendado en situaciones donde se requiere alta
precisión o en problemas tridimensionales.

En esta sección se describe un método para sumar vectores que
hacen uso de las proyecciones de un vector a lo largo de los ejes de
un sistema de coordenadas rectangular.

A estas proyecciones se las llama componentes del vector.
Cualquier vector se puede describir completamente por sus
componentes.


SUMA DE VECTORES: COMPONENTES ORTOGONALES

B
A

C


Cy By
B C

R
Ay A
Ry

Ax
Bx
Cx
Rx

       
Rx Ax Bx Cx Ry Ay By Cy

DETERMINACIÓN DE LA MAGNITUD Y DIRECCIÓN
DEL VECTOR R
Rx = Ax + B x + Cx (suma vectorial)
Ry = Ay + B y + Cy (suma vectorial)

R
Ry

Rx

2 2
Magnitud del vector R R R x R y

Línea de acción del 1
Ry
vector R
tan
Rx

Determine el vector que al sumarse a los
vectores a y b den una resultante nula.

a) i – 10j + 3k y
b) 2i – 5j + 6k
b a
c) 5j + 6k
5
d) 10j – 3k
x
e) –10j + 3k 3
7
z


y Solución:  a) i – 10j + 3k
a 7i 5 j b) 2i – 5j + 6k
b a  c) 5j + 6k
d) 10j – 3k
5 b 7i 5 j 3k e) –10j + 3k
x
  
7
3 a b c 0
z

Si un vector determinado vale cero, sus
componentes ortogonales valdrán cero también.

ax + bx + cx = 0 → cx = 0

ay + by + cy = 0 → cy = - 10 j
C = 0 i – 10 j + 3 k
Az + bz + cz = 0 → cz = 3 k

VECTOR EN 3-D Y LOS COSENOS DIRECTORES

y
Ax
Cos
A
Ay
Ay
Cos
A A
x
Ax
Az
Az
Cos
A
z

NOTAS IMPORTANTES SOBRE LA
DIRECCIÓN DE UN VECTOR
Si el vector se encuentra en el plano (2-D), la
dirección del vector será indicada a través del valor
del ángulo que forma el vector con el eje positivo de
las “x”.
Si el vector se encuentra en el espacio (3-D), la
dirección del vector será indicada por los ángulos
que forma el vector con cada una de las direcciones
positivas de los ejes de coordenadas.

RELACIÓN ENTRE LOS COSENOS DIRECTORES
Ax Ay Az
Cos Cos Cos
A A A Teorema de
A2 Pitágoras en
2 2
Ax Ay Az2

A2 ( ACos ) 2 ( ACos ) 2 ( ACos ) 2 3-D

A2 A2 Cos 2 A2 Cos 2 A2Cos 2

A2 A2 (Cos 2 Cos 2 Cos 2 )
Cos 2 Cos 2 Cos 2 1

Con esta expresión, si conocemos dos de los
tres ángulos podemos hallar el tercero.


y
A = 10 i – 8 j + 4 k 10 i

¿Cuál es la dirección
del vector A? A 8

-8j
A 102 82 42
x
4
z 10 4k
Ax 1 10
Cos cos 41,8o
A 13, 41

Ay 1 8 Az 4
Cos cos 126,6o Cos cos 1
72,6o
A 13, 41 A 13, 41


El vector mostrado en la figura tiene una
magnitud de 20 unidades. El ángulo que
forma el vector con el eje y es:
y
a) 30,0º

b) 60,0º
x
6
c) 72,5º 8
z
d) 41,1º

e) 35,2º


y Solución: Ay
Cos
A
x
¿Cuánto vale Ay?
6
8
z 2 2 2 2
A Ax A y A z

Ay 202 82 62 17,32

Ay 1 17,32
Cos cos 30o
A 20


EL PRODUCTO ESCALAR DE VECTORES
Sean A y B dos vectores y sea el menor ángulo formado
entre los vectores unidos por su origen

A
B

A • B = A B Cos
De acuerdo a la definición, A • B es un número
que puede ser positivo, negativo o cero, todo
depende del valor del ángulo entre los
vectores.

Proyección de un Vector: Producto Punto
 El producto punto nos dice
acerca de cuán paralelo son dos
vectores.
 El producto puntos (producto
escalar) de dos vectores puede
ser pensado como la proyección
de uno de los vectores sobre el

otro. B
 
A B AB cos ( A cos ) B 
A
 Componentes
A(B cos )
 
A B Ax Bx Ay By Az Bz

September 5, 2007

Proyección de un Vector: Producto Punto
 El producto punto nos dice
acerca de cuán paralelo
son dos vectores.
 El producto puntos (producto
escalar) de dos vectores puede
ser pensado como la proyección
de uno de los vectores sobre el 
otro. Projection is zero B
 
A B AB cos
 Componentes
  
A B Ax Bx Ay By Az Bz A

September 5, 2007

A

A•B=0
B
A
A•B <0
B

A
A•B >0
B


Dados los vectores A y B. En cuál de los siguientes casos
el valor de A•B tiene el mayor valor

1
A 2 3
B A B A

B


EL PRODUCTO ESCALAR EN COORDENADAS CARTESIANAS

SEAN LOS VECTORES: A = Ax i + Ay j + Az k y B = Bx i + By j + Bz k

A • B = (Ax i + Ay j + Az k) • (Bx i + By j + Bz k)

A • B = (Ax i) • (Bx i + By j + Bz k) + Ay j • (Bx i + By j + Bz k) + Az k •(Bx i + By j + Bz k)

El producto escalar entre vectores respectivamente
perpendiculares es igual a cero
A • B = Ax i • (Bx i) + Ay j • (By j) + Az k •(Bz k)

A • B = Ax Bx + Ay By + Az Bz

A = Ax i + Ay j + Az k y B = Bx i + By j + Bz k

A•B= Suma de los productos de sus respectivas componentes

A • B = Ax Bx + Ay By + Az Bz

¡TENGA CUIDADO CON LOS SIGNOS DE LAS
COMPONENTES DE LOS VECTORES!

A•B=B•A
EL PRODUCTO ESCALAR ES
CONMUTATIVO

INTERPRETACIÓN GEOMÉTRICA DEL PRODUCTO ESCALAR

A
Acos es la proyección del vector A
B sobre el vector B, esto es AB

El área del rectángulo que tiene
por lados A Cos y B, es AB Cos

AB Cos es por definición el resultado de
multiplicar escalarmente dos vectores de
magnitudes A y B que forman un ángulo .

A • B =ABB = BAA = AB Cos = Ax Bx + Ay By + Az Bz


Dado el siguiente gráfico:

P
S
Q

Entonces: S•P = S•Q

a) Verdad
b) Falso
c) Faltan los ángulos de los vectores

Para que los vectores: a = 6 i – 3 j + 6 k
y b = i – 2 j + 3 k sean ortogonales,
debe tomar el valor de

a) –4
b) 4
c) –6
d) 6
e) –8 α=-4


Sean lo vectores: a = 5i - 2j + 3k y
b = 2i + 5j + 6k. La proyección del
vector a sobre el vector b es.

a) 4.6
b) 3.2
c) 2.8
d) 2.2
e) 1.2
(5)(2) ( 2)(5) (3)(6)
ab 2, 23
2 2 2
2 5 6


Conociendo que |A| = 10 u y |B| = 15 u,
el ángulo formado entre los vectores
A y B es
y
a) 90,0º
b) 86,4º b
c) 80,4
d) 76,4º 5 x
a
e) 70,4º
z


Solución: |A| = 10 u y |B| = 15 u
y
B A • B = AB Cos = Ax Bx + Ay By + Az Bz

5 x Ax = 5 Ay = 0 Az = ?
A

z
Bx = 5 By = ? Bz = 0

A • B = AB Cos = (5)(5) + 0( By) + (Az)0

(10)(15) Cos = (5)(5)

1 25
cos 80, 4o
150


EL PRODUCTO CRUZ DE VECTORES
Sean A y B dos vectores y sea el menor ángulo formado entre
los vectores unidos por su origen.

   A
C AxB B

Se define el producto A x B como otro vector, llamemos C a
este vector. Por definición C es un vector perpendicular al
plano formado por los vectores A y B y su dirección está de
acuerdo a la regla de la “mano derecha”, la magnitud del
vector C es por definición:

C C AB Sen

La regla de la mano derecha y la
dirección del vector C

Cruce el vector A con el
vector B “barriendo” el
menor ángulo. El pulgar
extendido le da la
dirección del vector C


La Regla de la Mano Derecha

FLORENCIO PINELA - ESPOL 62 05/02/2010 23:47

C DIRECCIÓN DEL VECTOR C

AxB=C
B

A
BxA=-C
B

A AxB=-BxA
El producto vectorial
no es conmutativo!!!
-C

INTERPRETACIÓN GEOMÉTRICA DEL
PRODUCTO VECTORIAL

A
A Sen

B
  
A x B = C = AB sen

C = AB Sen => Área del paralelogramo formado
por los vectores A y B

Para la operación entre vectores C = AxB
indique si cada enunciado es correcto o no
1. (A x B) x C = 0 V F

2. C (A x B) = C2 V F
3. La proyección del vector A sobre V F
el vector C es cero
4. La proyección del vector C sobre V F
el vector B es diferente de cero

5. La magnitud del vector C V F
corresponde al área del paralelogramo formado de A y B
65 05/02/2010

Producto Cruz
 El producto cruz de dos
 Recall angular momentum
vectores nos dice acerca de   
cuán perpendiculares ellos son. L r p
Usted los encontrará en el  Torque
  
contexto de rotación o torque. r F
 
A B AB sin
 
B
 Dirección perpendicular tanto a B sin
A y B (regla de la mano-
 
derecha) A B B A   
A
ˆ ˆ ˆ 
i j k A sin
 
A B Ax Ay Az
Bx By Bz ( Ay Bz ˆ
Az By )i ( Az Bx Ax Bz ) ˆ ( Ax By
j ˆ
Ay Bx )k

EL PRODUCTO VECTORIAL EN COORDENADAS CARTESIANAS

SEAN LOS VECTORES: A = Ax i + Ay j + Az k y B = Bx i + By j + Bz k

A x B = (Ax i + Ay j + Az k) x (Bx i + By j + Bz k)

A x B = (Ax i) x (Bx i + By j + Bz k) + (Ay j) x (Bx i + By j + Bz k) + (Az k) x (Bx i + By j + Bz k)

El producto cruz de vectores que tienen la misma dirección vale cero!!

A x B = (Ax i) x (By j + Bz k) + Ay j x (Bx i + Bz k) + Az k x (Bx i + By j)

A x B = AxBy i x j + AxBz i x k + AyBx j x i + AyBz j x k + AzBx k x i + AzBy k x j


A x B = AxBy i x j + AxBz i x k + AyBx j x i + AyBz j x k + AzBx k x i + AzBy k x j
i j
ixj=k -k
jxk=i
i
kxi=j
k j i x k = -j k -j
j x i = -k

A x B = AxBy k + AxBz (-j) + AyBx (-k) + AyBz i + AzBx j + AzBy (-i)
Agrupemos los términos i, j y k

A x B = (AyBz – AzBy)i + (AzBx – AxBz)j + (AxBy – AyBx)k

A x B = (AyBz – AzBy)i + (AzBx – AxBz)j + (AxBy – AyBx)k

i j k
Ay Az Ax Az Ax Ay
AxB= Ax Ay Az = By Bz i - Bx Bz j + Bx By k
Bx By Bz


C ˆ j ˆ
( Ay Bz Az By ) i ( Ax Bz Az Bx ) ˆ ( Ax By Ay Bx ) k
 
       
 
Cx Cy Cz


Sean los vectores A y B no paralelos que se encuentran en un
mismo plano, se define C = AxB, entonces podemos afirmar que:

a) El modulo del vector C representa el área del triangulo formado
por A y B
b) La proyección vectorial de A sobre B es ( A.B ) / |B|
c) La proyección escalar de A sobre B es ( A.B )|B|
d) La proyección escalar de C sobre A es 0
e) No se puede realizar lo operación AxB


C = AxB En el grafico se indica que el vector C
F = ExD A es el resultado del producto vectorial
entre A y B y el vector F es el
F B resultado del producto vectorial entre
E y D.

E
Cuál de las siguientes opciones representa mejor la dirección de
un vector que sumado al vector (D x C) da una resultante nula.

A B C D

Sean los vectores A = 3 i – j + 2 k y B = -2 i – 2 j – 4 k, el
vector unitario perpendicular al plano formado por los
vectores A y B es
8 8
a )0i
128
j
128
k
Si logramos determinar un
8 8 8
vector perpendicular al plano
b)
192
i
192
j
192
k formado entre los vectores A y
B. Podemos determinar el
c)
1
i
11
j
8
k vector unitario dividiendo éste
186 186 186
vector para su magnitud.
8 8 8
e) i j k
384 384 384

8 16 8
e) i j k
384 384 384


Solución: A = 3 i – j + 2 k y B = -2 i – 2 j – 4 k

i j k
-1 2 3 2 3 -1
AxB= 3 -1 2 = -2 -4 i - -2 -4 j + -2 -2 k
-2 -2 -4

A x B = [(-1)(-4) - (-2)(2)] i – [(3)(-4) - (-2)(2)] j + [(3)(-2)-(-2)(-1)] k

C =Ax B = 8 i+ 8 j– 8 k

ˆ C 8i 8 j 8k
C
C 82 82 82

ˆ 8 8 8
C i j k
192 192 192

¿Cuál de las siguientes alternativas representa un
vector perpendicular al plano sombreado de la
figura?. y

6
a) 24i + 20j + 30k
b) –5i + 6j + 8k x
c) –12i – 10j + 15k 5
d) 12i – 10j –15k
e) 24i + 20j+ 15k 4
z


Solución:
6 Un vector perpendicular al
plano sombreado, es también
A x perpendicular al plano formado
5 por los vectores A y B
B
4
z A=6j–4k B=5i–4k
i j k
6 -4 0 -4 0 6
AxB= 0 6 -4 = 0 -4 i - 5 -4 j+ 5 0 k
5 0 -4

A x B = - 24 i – 20 j - 30 k

DETERMINE EL VALOR DEL ÀREA DEL PLANO
SOMBREADO DE LA FIGURA
y
Solución:
6
C = A x B = - 24 i – 20 j - 30 k

La magnitud de C representa A x
el área del paralelogramo 5
El área sombreada B
(rayada) corresponde a la 4
z 
mitad del área del C C 242 202 302
paralelogramo. 
C 43,3
Area sombreada 21,65 u 2
2 2

Dos vectores A y B vienen expresados por:
A = 3i + 4j + k ; B = 4i - 5j + 8k. Es verdad que A y
B:

a) Son paralelos y apuntan en la misma dirección.
b) Son paralelos y apuntan en direcciones contrarias.
c) Forman un ángulo de 45º entre sí.
d) Son perpendiculares.
e) Todas las alternativas anteriores son falsas.


Solución:

A = 3i + 4j + k y B = 4i - 5j + 8k.

Utilicemos la ley del coseno para determinar el ángulo
formado entre los vectores.
 
A B AB cos Ax Bx Ay By Az Bz

Ax Bx Ay By Az Bz
cos
AB

1 12 20 8 1 0
cos cos 90o
(26)(105) 2730


Sean las rectas AB y AC las que se cruzan en el punto A de
coordenadas (4,-5,6), y los puntos B y C de coordenadas
(2,3,5) y (5,4,2) respectivamente. ¿Cuál de las siguientes
alternativas representaría un vector perpendicular al plano
formado por las rectas?.

a) –23 i – 9 j – 26 k
b) 9 i – 14 j + 8 k
c) 9 i – 23 j + 26 k
d) 23 i – 9 j + 26 k
e) –9 i + 14 j – 8 k
= (-9+32)i – (-1-8)j + (8+18)k
= 23 i + 9 j +26 k
= - 23 i - 9 j – 26 k

Sean las rectas AB y AC las que se cruzan en el punto A de
coordenadas (4,-5,6), y los puntos B y C de coordenadas (2,3,5) y
(5,4,2) respectivamente.¿Cuál de las siguientes alternativas
representaría un vector perpendicular al plano formado por las
rectas?.
AC (5 4)i [(4 ( 5)] j (2 6)k C
AC i 9 j 4k

AB (2 4)i [3 ( 5)] j (5 6)k
AB 2i 8 j k

B

A

VECTORES: Bachillerato y Nivel Cero B (ESPOL)

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Viewers also liked

Viewers also liked (17)

Similar to VECTORES: Bachillerato y Nivel Cero B (ESPOL)

Similar to VECTORES: Bachillerato y Nivel Cero B (ESPOL) (20)

More from ESPOL

More from ESPOL (20)

Recently uploaded

Recently uploaded (20)

VECTORES: Bachillerato y Nivel Cero B (ESPOL)